Modèle géométrique
Modèle géométrique direct
Connaître le modèle géométrique direct (MGD) d'un robot correspond à pouvoir exprimer :
- à partir des coordonnées d'un point vecteur exprimées dans le repère effecteur du robot
- les coordonnées du même point / vecteur exprimées dans le repère de travail du robot
- en fonction des coordonnées articulaires
La MGD se ramène donc à la matrice de transformation homogène , lors du calcul du MGD sur un robot nous pouvons faire face à des calculs de grande complexité oou très redondants. Il est donc nécessaire de choisir un langage commun pour la faire transparaître. Ce langage est la normalisation de Denavit-Hartenberg. :
- Règles imposées de choix des axes et origines
- Unicité des transformations homogènes
- Un et un seul repère lié à chaque articulation
Sur l'exemple du robot ABB ci dessous la formalisme de Denavit-Hartenberg est utilisé pour exprimer les transformations homogènes :
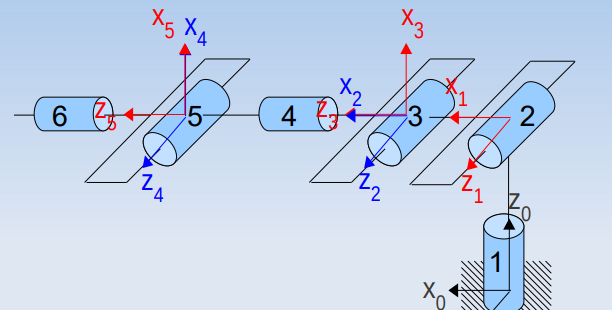
Ce formalisme se résume par le tableau de Denavit-Hartenberg
| 0,1 | ||||
| 1,2 | ||||
| 2,3 | ||||
| 3,4 | ||||
| 4,5 | ||||
| 5,6 |
Modèle géométrique inverse
Le MGD permet de déterminer l'orientation et la position de l'effecteur du robot, en fonction des variables articulaires . Le MGI permet de déterminer les variables articulaires en fonction de l'orientation et la position de l'effecteur du robot. Le MGI n'est pas l'inversion de la matrice !
Le calcul direct est trop complexe, en effet pour obtenir la posture désirée du robot, il suffit d'écrire l'égalité entre :
- exprimée en fonction des coordonnées articulaire ()
- La posture désirée
Méthode de PAUL
Nous faisons le constat que l'équation est composé d'une expression souvent simple à gauche et souvent très complexe à droite. Le but de la méthode de Paul est de simplifier cette expression à droite. Plus particulièrement, il s'agit de les exprimer dans un autre repère que 0 pour permettre aux de n'appaître qu'une seule fois dans l'équation. Certaines équations sont caractéristiques et forment 8 types facile à résoudre présent en annexe.