Calcul quantique, algorithme de Deutsch
Ordinateur classique vs ordinateur quantique
On peut schématise un ordinateur classique (machine de Turing) à l'aide de 3 composants,
- des registres (qui contiennent les données à traiter)
- une unité de calcul (qui transforme les données suivant un algorithme défini en actionnant des portes logiques)
- une unité d'entrées/sorties (qui initialise les registres au début du traitement et lit les résultats à la fin)
Les registres
- les registres classiques sont un ensemble de bits permettant de stocker entiers entre 0 et .
- un registre quantique est un système quantique de qubits dont les états seront éléments de l'espace des états de dimension . On définit dans cet espace la base
- Liste des états de chaque qubit, éléments de :
- nombre entier dont l'ensemble constitue la décomposition binaire
est l'ensemble des entiers modulo tel que
Spécificité des registres quantiques
Les registres quantiques peuvent se trouver non seulement dans un des états de la base (comme le registre classique), mais aussi dans un état de superposition
Les algorithmes quantiques sont représentés par l'évolution d'un ou plusieurs registres sous l'effet de l'application d'opérateurs unitaires. L'état de l'ordinateur peut comprendre plusieurs registres.
Les entrées / sorties
L'entrée correspond à mettre le système quantique lui même constitué par les registres dans un état initial, on dit qu'on prépare le système. Le plus souvent les différents registres sont initialement dans l'état , et la préparation consiste à faire agir différents opérateurs, comme la transformation de Hadamard.
La sortie correspond à la lecture d'un registre mesure de l'état quantique final du registre. D'après (le postulat de la mesure de la mécanique quantique) il la modifie, et de façon irréversible, l'état du registre (qui est projette sur 1 des états de la base). En général, les algorithmes quantique utilisent des mesures partielles de l'état final (mesure de seulement un des registres, voir même quelques bits d'un registre)
Parallélisme quantique
Souvent on a besoin d'évaluer la fonction
qu'on ne peut pas toujours représenter par un opérateur unitaire. Pour associer un opérateur unitaire à l'évaluation d'une fonction, on introduit une fonction et on définit
- un registre de données à qubits, contiendra la valeur de la varible
- un registre de résultats à qubits, contiendra le résultat
- un opérateur unitaire
Le parallélisme est un trait de beaucoup d'algorithme quantique une fonction peut être évaluée simultanément en plusieurs valeurs de (conséquence de la superposition des états de qubits)
Exemple
Soit un registre donné et un registre de résultats chacun à 1 qubit. La valeur initiale de chaque registre est
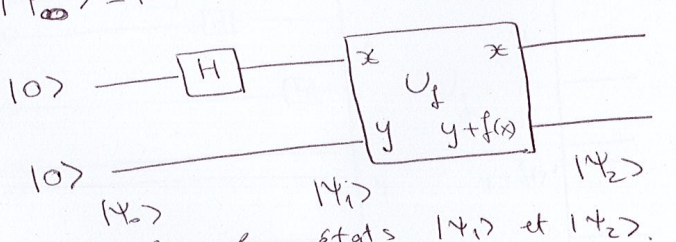
Exercice : calculer les états et
on effectue l'application de la porte de Hadamard sur 2 qubits
L'état de sortie est
Il contient ) la fois et obtenues par une seule application de la porte
Généralisation
Soit un registre à qubits (registre de données). La transformation / porte de Hadamard sur chaque qubit donne pour le registre de données
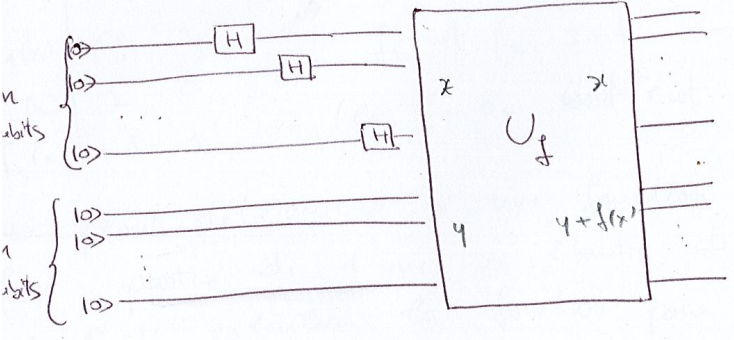
Les états de sortie sont
Cela fait apparaître de nouveau toutes les valeurs de en une seule opération, c'est le parallélisme quantique.
Algorithme de Deutsh (1985)
L'algorithme de Deutsh-Jozsa est un algorithme quantique, proposé par David Deutsh et Richard Jozsa en 1992. Dans le cas du problème de Deutsh-Jozsa, nous disposons d'une boite noire quantique, connu sous le nom d'oracle qui implémente une fonction mathématique . Nous savons que cette fonction est soit constante (la sortie est 0 ou 1 pour toutes les entrées) soit équilibrée (la sortie est 0 dans la moitié des cas, 1 dans les autres). Le but du problème est de savoir si la fonction est constante ou équilibrée à l'aide de l'oracle.