Intrication quantique
Rappels : produit tensoriel de qubits
Produit tensoriel et qubits
Représentation matricielle des qubits
Cas particuliers
et
Produit tensoriel de matrices
Produit tensoriel de qubits - Exercice
Calculer les produits tensoriels des états et .
L'intrication quantique
L'intrication quantique est un caractère subtile et paradoxal de la mécanique quantique (paradoxe EPR)
États à 2 qubits
Soit le qubit et et soit le qubit et états du système chaque qubit se trouve dans un état de superposition :
- qubit
- qubit
Système . Notation les états
La mécanique quantique nous dit (1 er postulat) que tout état à 2 qubits se décompose
avec
L'état est un état factorisé
Il existe des états qui ne se factorisent pas a un produit d'états à 1 qubit états intriqués. Ce sont des états spécifiques de la description quantique, ils engendrent entre les particules des corrélations fortes qui sont à la base des différents protocoles et algorithmes de l'informatique quantique.
Important : dans ces états, l'état individuel d'un qubit n'est pas défini, c'est le système qui est dans un état défini.
Les états intriqué - 1er état de Bell
Tant qu'aucune mesure n'est eeffectuée sur le système, l'état de chaque qubit n'est pas défini. Si nous mesurions le 1er qubit etn ous trouvons l'état , alors l'état est projeté sur l'état ce qui entraîne que le 2ième qubit est forcément lui aussi dans l'état .
On suppose qu'il existe tel que
\begin{align} \vert \beta_{00} \rangle &= (\alpha_0 \vert 0 \rangle + \alpha_1 \vert 1 \rangle )(\beta_0 \vert 0 \rangle + \beta_1 \vert 1 \rangle) \\ &\Leftrightarrow \dfrac{1}{\sqrt{2}} \vert 00 \rangle + \dfrac{1}{\sqrt{2}} \vert 1 1 \rangle = \alpha_0 \beta_0 \vert 00 \rangle + \alpha_0 \beta_1 \vert 01 \rangle + \alpha_1 \beta_0 \vert 10 \rangle + \alpha_1 \beta_1 \vert 11 \rangle \\ &\Rightarrow \alpha_0 \beta_0 = \dfrac{1}{\sqrt{2}} = \alpha_1 \beta_1 \Rightarrow \alpha_0, \beta_0, \alpha_1, \beta_1 \neq 0 \\ &\Rightarrow \alpha_0 \beta_1 = 0 = \alpha_1 \beta_0 \end{align}
Cela conduit à une contradiction donc en somme l'état de Belle ne se factorise pas, l'état de Belle est un état intriqué.
Mesure d'un état à 2 qubits
D'après la mécanique quantique (d'après le postulat de la mesure), si on mesure l'état de 2 qubits, le système est projeté dans l'un des états de base ou avec une probabilité .
Mesure partielle
On mesure uniquement un des 2 qubits, la mesure va fixer l'état du qubit mesure. L'état du système sera une superposition des états de base compatibles, et dans laquelle le qubit mesuré aura une valeur fixée.
Par exemple, si on mesure le 1er qubit du système de l'état (2) et on trouve , le système est projeté dans l'état
Téléportation quantique
On parle ici de la téléportation d'état quantique et pas de la téléportation de système physique porteur de l'état. Pour réaliser la téléportation quantique il faut une paire de particules intriqués. En revanche l'état initial, qui est téléporté, est détruit ! Cela est une différence avec le clonage quantique.
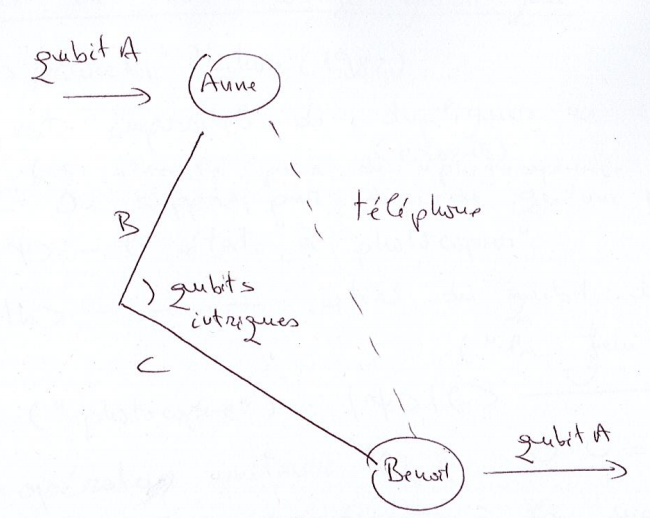
Illustration
Comment transmettre d'un point à un point le contenu inconnu d'un qubit (ie d'un état quantique) ? (le système physique porteur du qubit n'est pas transporté !).
- A et B se sont offert antérieurement un des 2 qubits d'un état intriqué de Bell
- A veut transmettre à B le contenu d'un qubit dans un état que A ne connait pas.
- système à 3 qubits :
Ordre de qubits :
- A le qubit inconnu
- B le le 1er qubit de la paire intriqué (détenu par Anne)
- C le 2nd qubit de la paire intriqué (détenu par Benoît)
A réalise les opérations suivantes
- A réalise un CNOT sur la paire (A,B), A obtient
- A envoie le 1er qubit sur une porte de Hadamard, l'état du système devient
\begin{align} \vert \Psi_2 \rangle &= \dfrac{1}{2} [\alpha (\vert 1000 \rangle + \vert 011 \rangle + \vert 111 \rangle) + \beta (\vert 010 \rangle - \vert 110 \rangle + \vert 1001 \rangle - \vert 101 \rangle)] \\ &= \dfrac{1}{2}(\vert 00 \rangle (\alpha \vert 0 \rangle + \beta \vert 1 \rangle) \\ &+ \vert 01 \rangle (\alpha \vert 1 \rangle + \beta \vert 0 \rangle) \\ &+ \vert 10 \rangle (\alpha \vert 0 \rangle ( \beta \vert 1 \rangle ) \\ &+ \vert 11 \rangle (\alpha \vert 1 \rangle - \beta \vert 0 \rangle))) \end{align}
L'état du qubit est complètement déterminé par celui de la paire , détenu pour A, c'est un effet de la corrélation quantique due à l'intrication de la paire .
- A lit (mesure) la paire (A,B) et transmet le résultat à B par téléphone (informatique classique), la téléportation ne viole par la relativité restreinte d'Einstein (aucune info ne peut être transmise plus vite que la lumière !)
- Benoît reçoit le résultat de A, B réalise sur un qubit C l'opération
On peut vérifier que l'état résultant du qubit C est
l'état !
Théorème de non-clonage quantique
(Wooters, Zurek, Nature)
Il est impossible de dupliquer un état quantique
On suppose par l'absurde, qu'une telle "machine" existe. Soit l'état à photocopier et l'état initial du qubit de copie. Le clonage consiste à réaliser l'opération suivante
Soit un autre état à cloner,
\begin{align} &\Rightarrow \vert \phi \rangle \vert \phi \rangle = \cup \vert \phi \rangle \vert b \rangle \equiv \langle \phi \vert \langle \phi \rangle = \langle b \vert \langle \phi \vert \cup^+ \\ &\Rightarrow \langle \phi \vert \langle \phi \vert \vert \psi \rangle \vert \psi \rangle = \langle b \vert \langle \phi \vert \cup^+ \cup \vert \psi \rangle \vert b \rangle \\ (\langle \phi \vert \psi \rangle)^2 &= \langle b \vert b \rangle \langle \phi \vert \psi \rangle \\ &\Rightarrow (\langle \phi \vert \psi \rangle)^2 = \langle \phi \vert \psi \rangle, \forall \vert \phi \rangle, \vert \psi \rangle \\ &\Rightarrow \langle \phi \vert \psi \rangle = 1, \forall \vert \psi \rangle, \vert \psi \rangle \text{contradiction}\\ &\Rightarrow \langle \phi \vert \psi \rangle = 0, \forall \vert \psi \rangle, \vert \psi \rangle \text{états orthogonaux -> contradiction} \end{align}
Il est donc impossible de cloner des états quantiques
Manipulation d'état à 2 qubits - Calcul quantique
Les opérateurs sur 1 ou plusieurs qubits correspondent à l'action d'opérateurs unitaires -- évolutions réversibles (différence fondamentale avec les ordinateurs classiques -- évolutions irréversibles). Dans le monde classique, nous avons le théorème de la logique classique : toute porte logique peut être construire à partir de NAND et COPY. NAND et COPY ne peuvent pas être transposé dans le quantique à cause de l'irréversibilité et du théorème de non clonage quantique). Cependant, il est possible de transformer les algorithmes classiques irreversibles en algorithme réversibles.
Cependant cela a un cout
- Augmentation du volume d'information traitée
- Introduction d'un nouvelle porte à 3 bits, TOF (porte de Toffoli)
On dit qu'une fonction est calculable, "avec variables auxiliaire" sur l'ensemble de portes (réversibles) si et seulement si il existe un circuit à entrée tel que
c'est à dire le circuit se sert des dernière places pour calculer, mais ne prend aucune donnée, ni ne retourne aucun résultat, dans ces places.
On peut montrer que tout circuit irréversible calculant une fonction peut être transformé en circuit réversible, avec variable auxiliaires calculant . À travers cette équivalence, on pourra associer un algorithme quantique réversible à tout algorithme classique irréversible.
Théorème de Bennet-Landoueur - Toffoli
Soit . Toute application booléenne inversible
est calculable par un circuit (avec variables auxiliaire sur l'ensemble des portes NOT,SWAP,TOFF). La porte NOT peut être remplacée par la porte cNOT
| entrée | sortie | | 00 | 00 | | 01 | 01 | | 10 | 11 | | 11 | 10 |
1er bite de controle la valeur est inchangée. Le deuxième bit est le bit cible, sa valeur est inchangée si le bit de contrôle vaut 0 et il est inversé si le bit de controle vaut 1.
Le cNOT quantique est représentée par une matrice dans la base .
Théorème de Kitaev-Shen-Vialyi
Soit . Toute matrice unitaire , vue comme une porte à -qubits, est calculée par un circuit sur l'ensemble de portes
Les portes reversibles de bases (traduits en transformations unitaires) ainsi que toutes les portes à 1 qubit, contrôlés par un autre qubit, suffisant pour calculer n'importe qu'elle transformation unitaire sur qubits