Skip to main content

TD - Feuille 2

Notes inspirées du cours de JANIN David et du TD2 de Myriam Desainte-Catherine

Grammaires​

Étant donné une grammaire GG de non terminal initial SS (start symbol) et d'alphabet terminal TT, on appelle langage défini par SS le langage

L(G)={w∈T∗∣S→∗w}L(G)=\{w \in T^\ast \vert S \rightarrow^\ast w\}

c'est à dire l'ensemble des mots de terminaux qui décrivent du non terminal initial.

Exerice 1​

Proposer une grammaire qui permet, sur l'alphabet de terminaux {a,b}\{a,b\} de définir le langage des mots de la forme anbna^n b^n avec n∈Nn \in \mathbb{N}. Votre grammaire est-elle ambigüe ?

S -> aSb
S -> eps

Exercice 2​

Soit la grammaire

(0) S -> e //mot vide
(1) S -> aB          (2) S -> bA
(3) A -> aS          (4) A -> bAA
(5) B -> bS          (6) B -> aBB

définie avec les terminaux {a,b}\{a,b\}, les non-terminaux {S,A,B}\{S,A,B\} et le start symbol SS

  • Construire les arbres de dérivation de abba et aabb

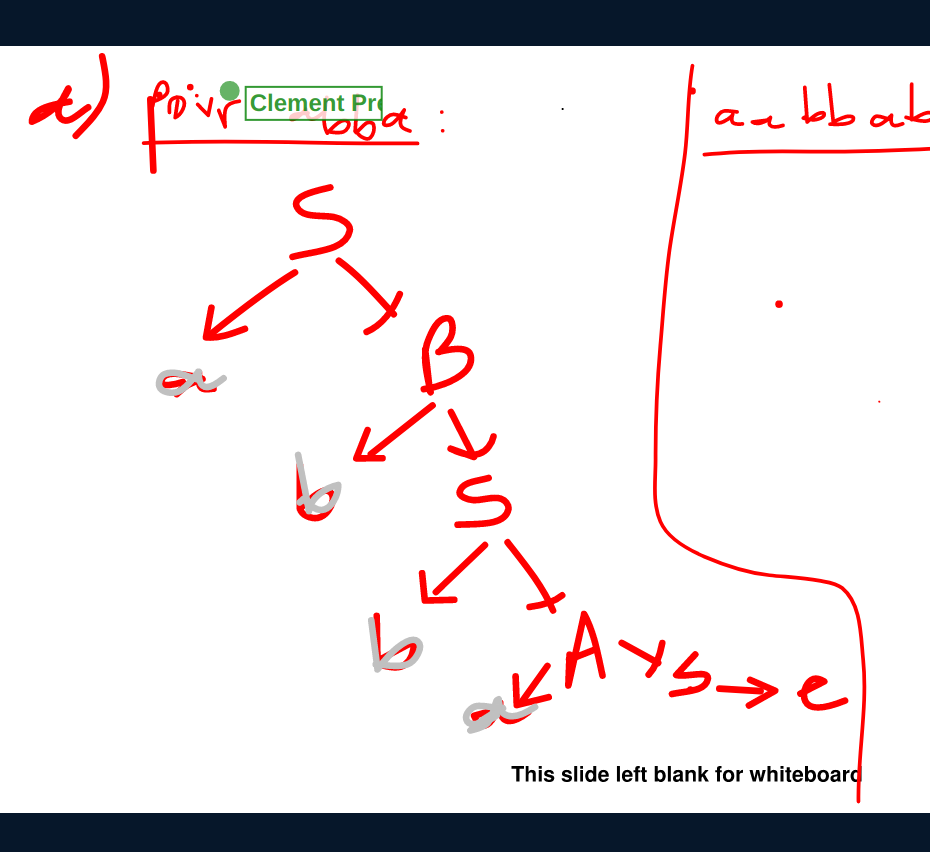
  • Cette grammaire est elle ambigüe ?

Elle n'est pas ambigüe

  • Quel langage définit-elle ?

(S)={ab,ba,ε,...}(S) = \{ab,ba,\varepsilon,...\} (A)={a,aab,aba,...}(A) = \{a, aab, aba, ...\} (B)={b,bab,bba,...}(B) = \{b,bab,bba,...\}

Conditionnelles​

On considère la grammaire COND définie par :

I -> nop | C
C -> if B then I | if B then I else I
B -> id | true | false

avec les non-terminaux II (instructions), CC (instructions conditionnelles), BB (booléens) et les terminaux id, true, false, nop, if, then et else.

Exercice 3​

Quel est le langage défini par cette grammaire ? Construire un arbre de dérivation pour if id then if id then nop else nop. En existe-t-il un autre ? Qu'en déduire ?

Nous pouvons soupçonner que la grammaire est ambigüe, en effet nous avons deux arbres de dérivations possibles

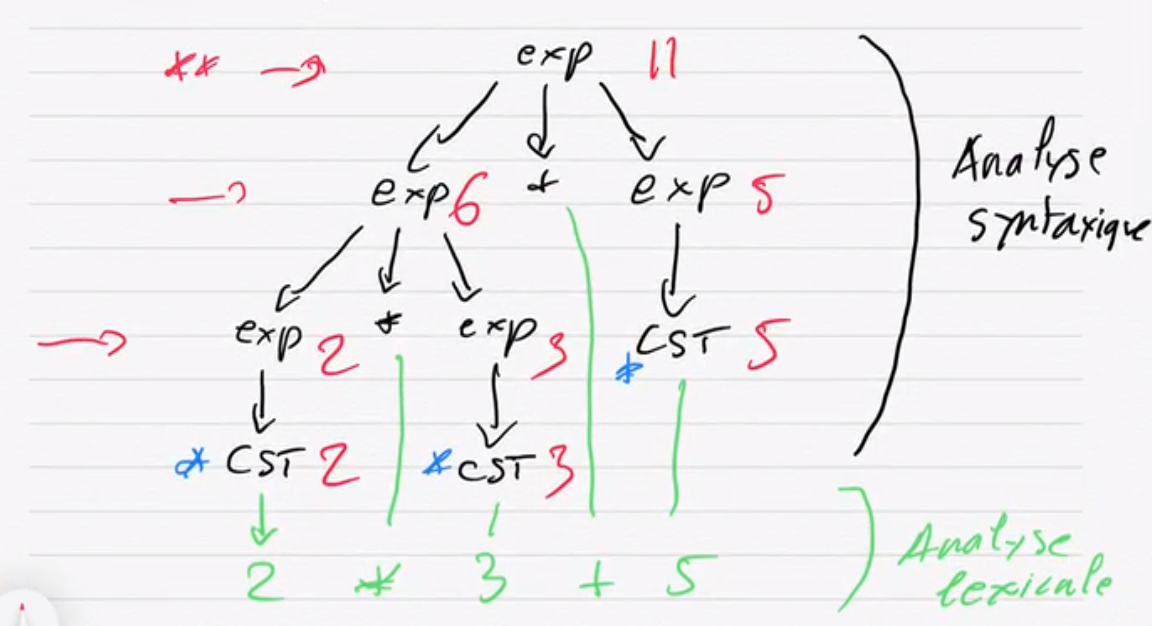
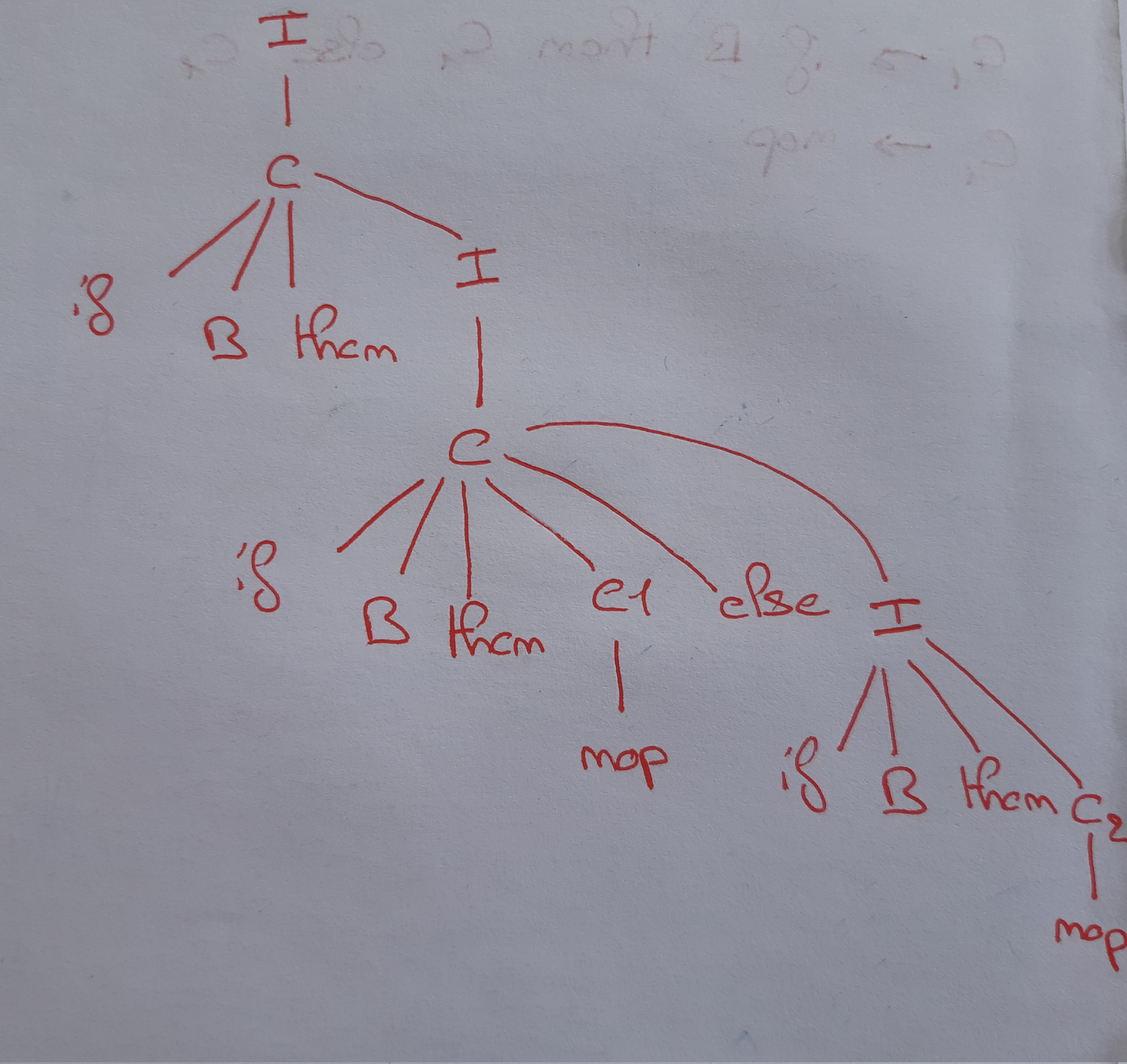
Exercice 4​

Proposer une grammaire non ambigüe permettant de définir le même langage. Votre grammaire devra, comme dans le langage C, “forcer” l’association du “else” avec le “if-then” qui précède le plus proche qui n’est pas déjà “fermé” par un “else”.

Pour éliminer l'ambiguïté il faut réecrire la grammaire :

C1 -> if B then C1 else C1
C1 -> nop

Expressions arithmétiques​

Exercice 5​

A -> id = E
E -> T
E -> E + T
T -> F
T -> T * F
F -> id
F -> cst
F -> (E)
  • Dessiner les arbres de dérivaitions ainsi que numéroter les noeuds de l'arbre de dérivation dans l'ordre du parcours de l'analyseseur (postfixe)

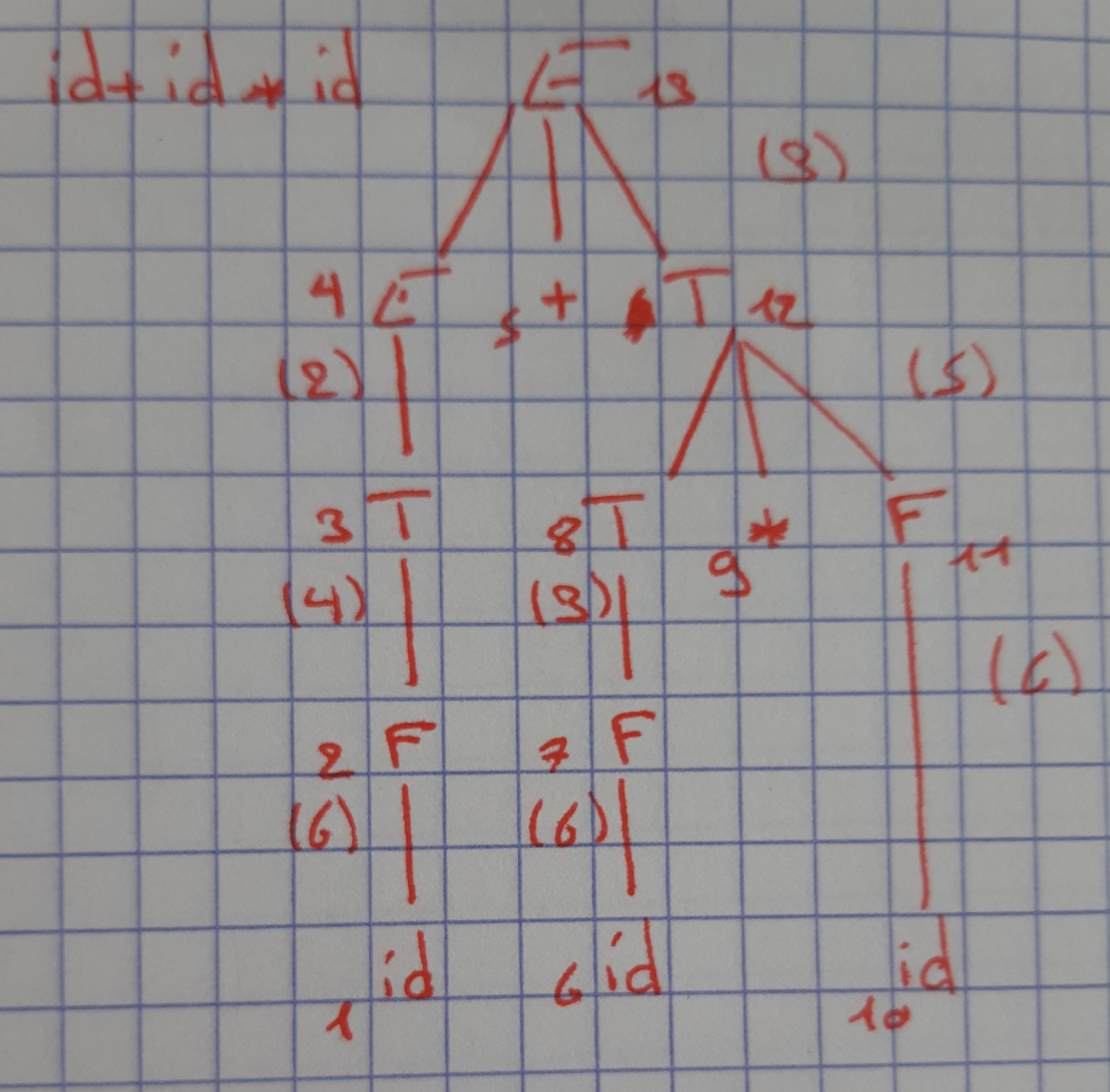
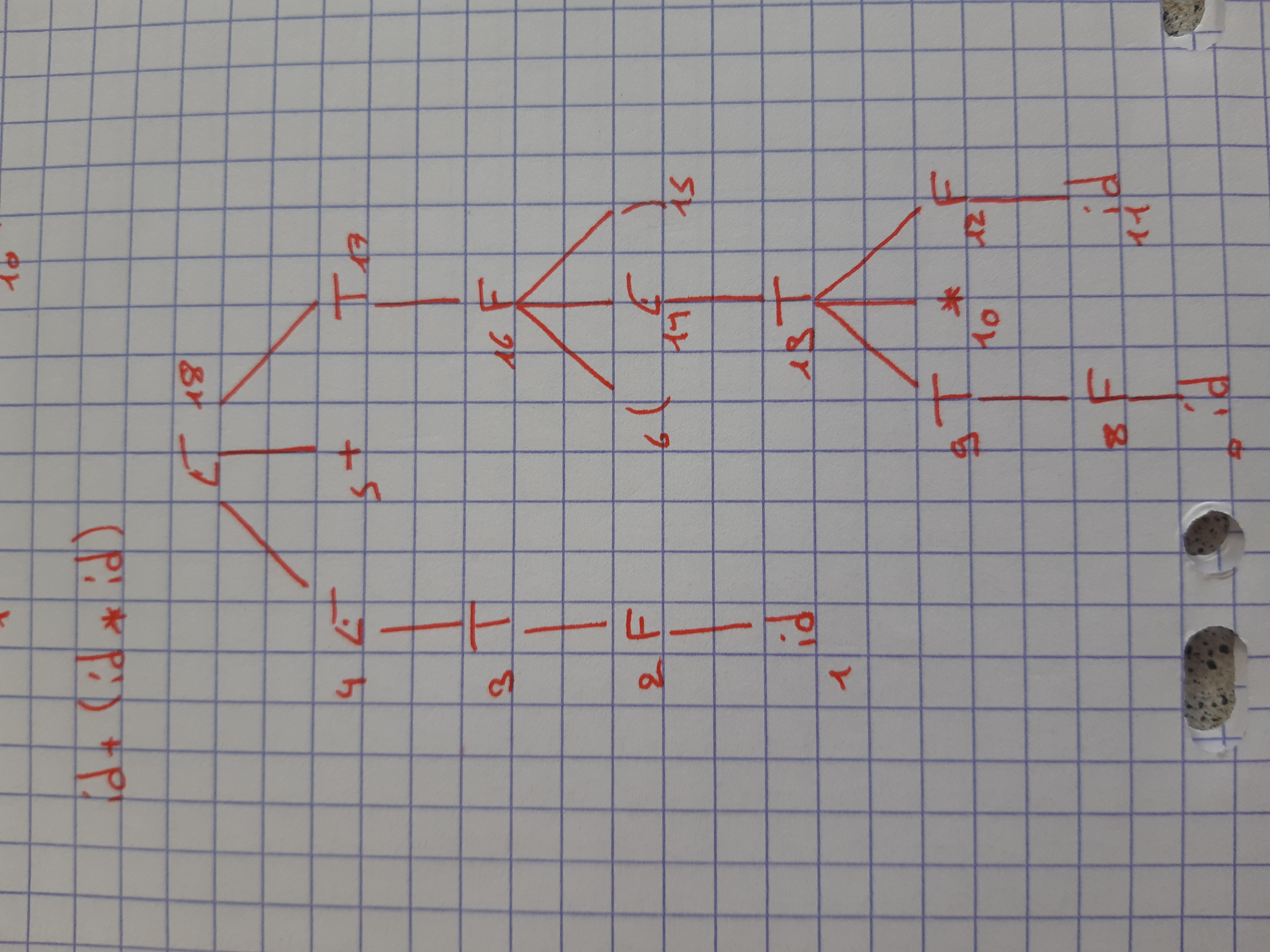
  • Écrire les actions sémantiques associées à chaque règle qui permettent de traduire une expression arithmétique en code 3 adresses
1. {$$=newreg();printf("r%d=%s\n";$$,$0);}
2. $$=$1
3. {$$=newreg();print("r%d= r%d + r%d \n", $$, $1, $3);}
4. $$=$1
5. {$$=newreg(); printf("r%d = r%d * r%d",$$,$1,$2);}
6. {$$=newreg();printf("r%d=%s\n";$$,$1);}
7. {$$=newreg();printf("r%d=cte\n";$,$1);}
8. $$=$2
0%