Vidéo 5

Question du jour : Que faire avec les arbres de dérivation ?

Sur un exemple : les expressions arithmétiques

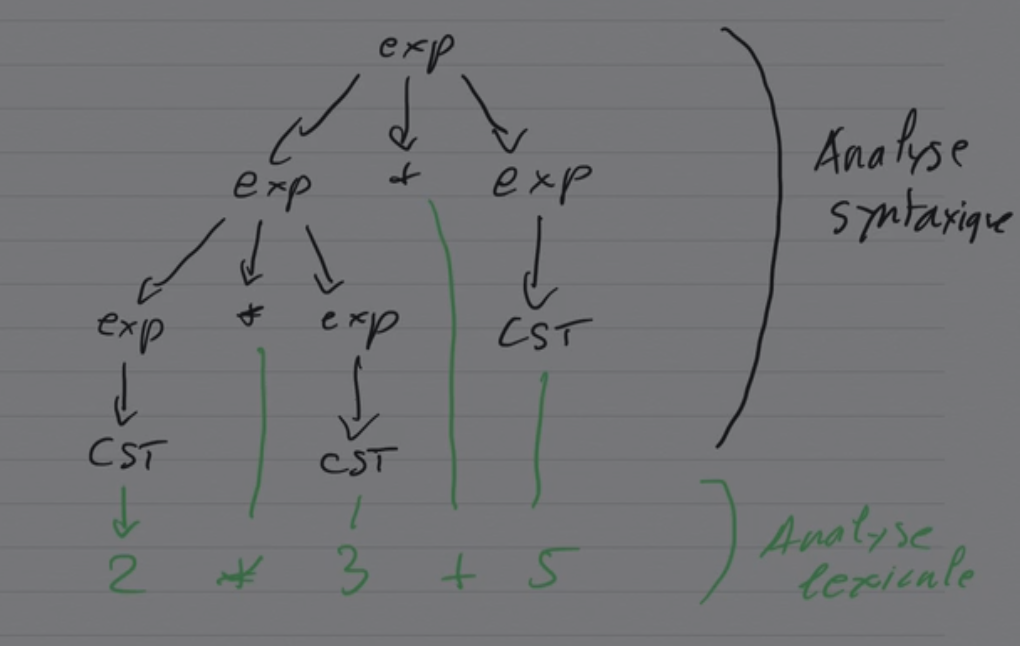
Comment évaluer cette expression ? Il suffit d'effectuer une évaluation des feuilles vers la racine

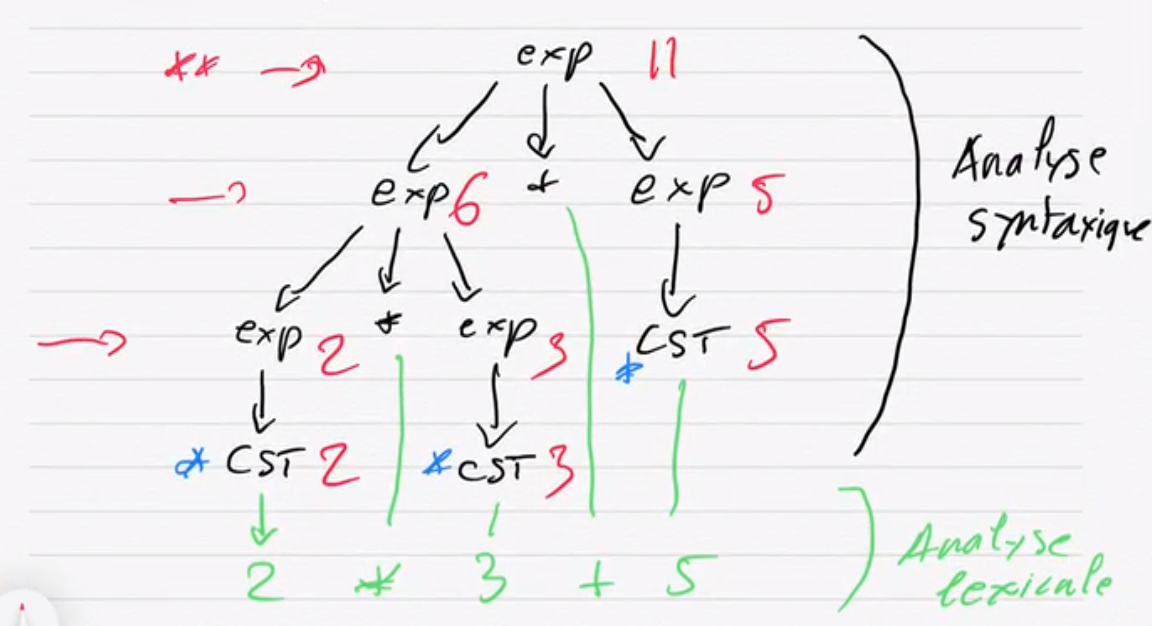
** : les valeurs sont obtenue par application d'une règle de calcul, la valeur d'un noeud interne dépendant des valeurs (tout ou partie) portées par ses enfants (Dans l'analyse syntaxique).

Remarques

Les règles de calcul a utiliser ne dépendent que des règles de grammaires utilisés. Les calculs sont locaux et uniformément défini par la règle appliquée.

Plus généralement, ces valeurs associées aux noeuds des arbres de dérivations sont appelés attributs. Dans l'exemple, on parle d'attribut synthétisé, puisque pour chaque règle de la forme

$X \rightarrow x_1, x_2, ..., x_n$ la valeur d'attribut de $X$ dépend des valeurs d'attributs de $x_1,...,x_n$ .

Dans le cas général, la théorie des grammaires attribuées, les dépendance entre attributs, peuvent être plus complexe, cela génère des équations, pouvant être difficile à résoudre.

Exemple utile : dans une règle $X \rightarrow x_1, x_2, ..., x_n$ on peut souhaiter que l'attribut de $x_{i+1}$ dépende aussi de l'attribut de $x_i$ . Nous verrons comment faire cela avec des attributs synthétisés (calculs des feuilles vers la racine) + effet de bords

Attention : dans tous les cas, la règle de calcul a appliquer ne dépend que de la règle de grammaire à la quelle elle est associée.

Remarque : Dans l'exemple les attributs, prennent la "valeur entière" de leur noeud. Un attribut pourra aussi être :

un type
des numéros de registres (pour la production de code)
des morceaux de code
...

Ou une combinaison des choses ci-dessus en définissant les valeurs d'attributs comme des $n$ -uplets (struct en C).

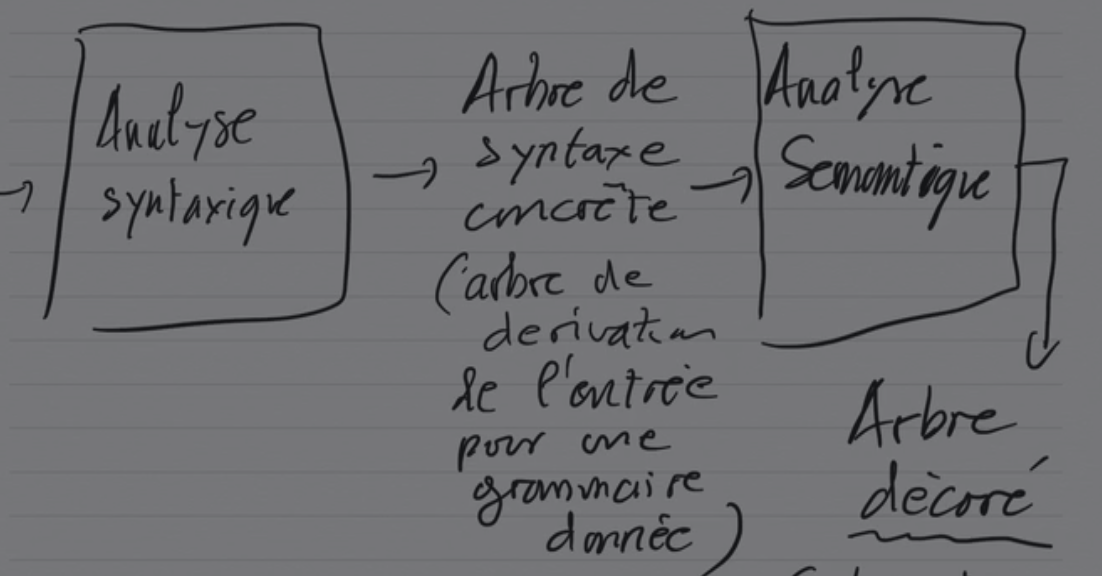
En Yacc, trois choses sont

Pour désigner les attributs dans une règle de la forme $X \rightarrow x_1, x_2, ..., x_n$ $X \to x_{1}, x_{2}, ..., x_{n}$ avec $x \in N$ $x \in N$ et $x_1, x_2, ..., x_n \in N \cup T$ $x_{1}, x_{2}, ..., x_{n} \in N \cup T$ . On désignera par
- $ la valeur d'attribut de $X$
- $1, $2,..., $n les valeurs d'attributs de $x_1,...,x_n$ dans cet ordre (de gauche à droite)
La règle de calcul de l'attribut de $x$ en fonction des attributs, des terminaux et non terminaux du membre droit, sera écrite en $C$ , à la suite de la règle $X \rightarrow x_1,x_2, ... x_n \underbrace{\{\$\$ = f(\$1,\$2,...,\$n);\}}_{\text{action sémantique}}$ On voit ici que le calcul à faire est définit règle par règle de grammaire.
L'arbre de dérivation est construit des feuilles vers la racine, de gauche à droite. De façon équivalente, tout se passe comme si on faisait un parcours en profondeur, à gauche, postfixe. C'est en sortant d'un sous arbre qu'on exécute l'action sémantique. Autrement dit, pour un arbre de dérivation donné, l'ordre d'exécution des actions sémantiques est non-ambigüe (exécution postfixe). Conséquence : les actions sémantiques étant du code C avec des effets de bords possible, on pourra aussi communiquer des valeurs d'attributs de la gauche vers la droite des arbres de dérivation.

Mise en oeuvre sur notre exemple des expressions arithmétiques.

exp -> CST
exp -> ID
exp -> exp + exp
exp -> exp * exp
exp -> (exp)

Écrire des actions sémantiques (des calculs d'attributs) permettant d'évaluer les expressions arithmétiques. On supposera que les attributs des terminaux sont des chaînes de caractères C contenant les valeurs lexicales associées

Remarques​

Remarques