Graphe - Abres
Union Find
On dispose d'ensembles disjoints sur éléments, on veut
- Tester si 2 éléments appartiennent au même ensemble ?
Find(x)=Find(y) - Fusionner 2 ensembles disjoints contenant et
Union(x,y)
Une première structure naïve
Question 1
Test si et appartient au même ensemble en temps
Question 2
UNION : Tous les éléments de l'ensemble de doivent mettre à jour leur indice z.indice = y.indice en temps linéaire en fonction de
Question 3. Complexité totale
Vers une version efficace
Question 4
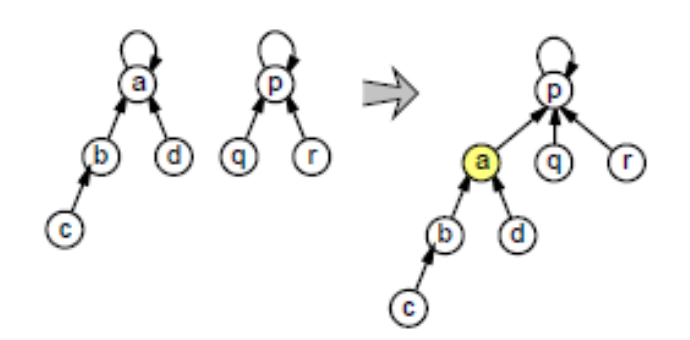
Question 5
La complexité de la séquence Union(1,2)...Union(1,n) est
Question 6
On a
Question 7
On va utiliser le principe de récurrence forte: Soit une propriété définie sur , si
- .
- (pour tout )
alors pour tout entier .
Soit la proposition: “Tout ensemble dont la racine est de rang r possède au moins éléments”. Supposons que soit vérifiés. Soient 2 ensembles et de rang et . Si , le rang de l’union est inférieur à , hypothèse vérifiée. Si , le rang de l’union est . l’ensemble possède au moins . Si , le rang de l’union est , l’ensemble possède au moins . On a vérifiée. Il s’agit de l’unique cas où le rang dépasse . Dans tous les cas, on a que implique .
Question 8
Par récurrence, on sait que si une racine est de rang alors son ensemble possède au moins éléments (question 7). Or donc . Comme il y a croissance du rang dans un chemin qui va vers la racine, on a que la hauteur maximale de l’arbre est donc . Toute opération FIND et UNION prend un temps . Chaque opération MakeSet prend un temps . Ainsi la complexité est .
Notons qu’on peut encore améliorer la structure avec une opération simple de compressions de chemins pour diminuer encore la profondeur de l’arbre.