Automates finis et application - TD1
Langages et automates finis
Exercie 1
Pour chaque langage ci dessous sur l'alphabet donnez un automate fini déterministe qui l'accepte.
Le nombre de est un multiple de 4.
![1.1]
Un nombre pair de et impair de .
![1.2]
Tout symbole est précédé et suivi d'au moins un symbole
![1.3]
Exercice 2
Pour chaque langage ci dessous sur l'alphabet binaire , donnez un automate fini déterministe qui l'accepte :
Les entiers pairs
![2.1]
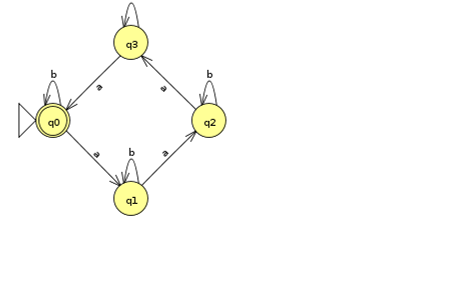
Les entiers multiples de 3
![2.2]
Exercice 3
Pour chaque langage ci-dessous sur l'alphabet , donnez un automate fini non déterministe qui l'accepte
Les mots qui se terminent par
![3.1]
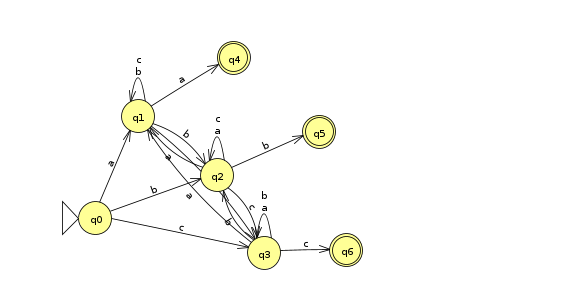
Les mots dont la dernière lettre apparait précédemment dans le mot
![3.2]
Les mots dont la dernière lettre n'apparait pas précédemment dans le mot
![3.3]
Exercice 4
Ecrire un algorithme qui indique si un automate fini détermininste et complet accepte un mot
Formellement soit un mot ( est la ième lettre du mot) et un automate, on veut décider si est accepté par . Soit l'ensemble des états que l'on peut atteindre en ayant lu
X_0 = q_0
pour i de 1 à k
X_i != 0
pour tout p dans X_{i-1}
pour tout q tel que (p,w_i,q) est dans E
X_i=X_i u {q}
pour tout p dans X_k
si p est dans F
retourner Vrai
retourner Faux
Exercice 5
L'idée est de supprimer les deux états initiaux et d'en créer un nouveau qui
mêne aux deux anciens

Exercice 6
Démonstration par l'exemple
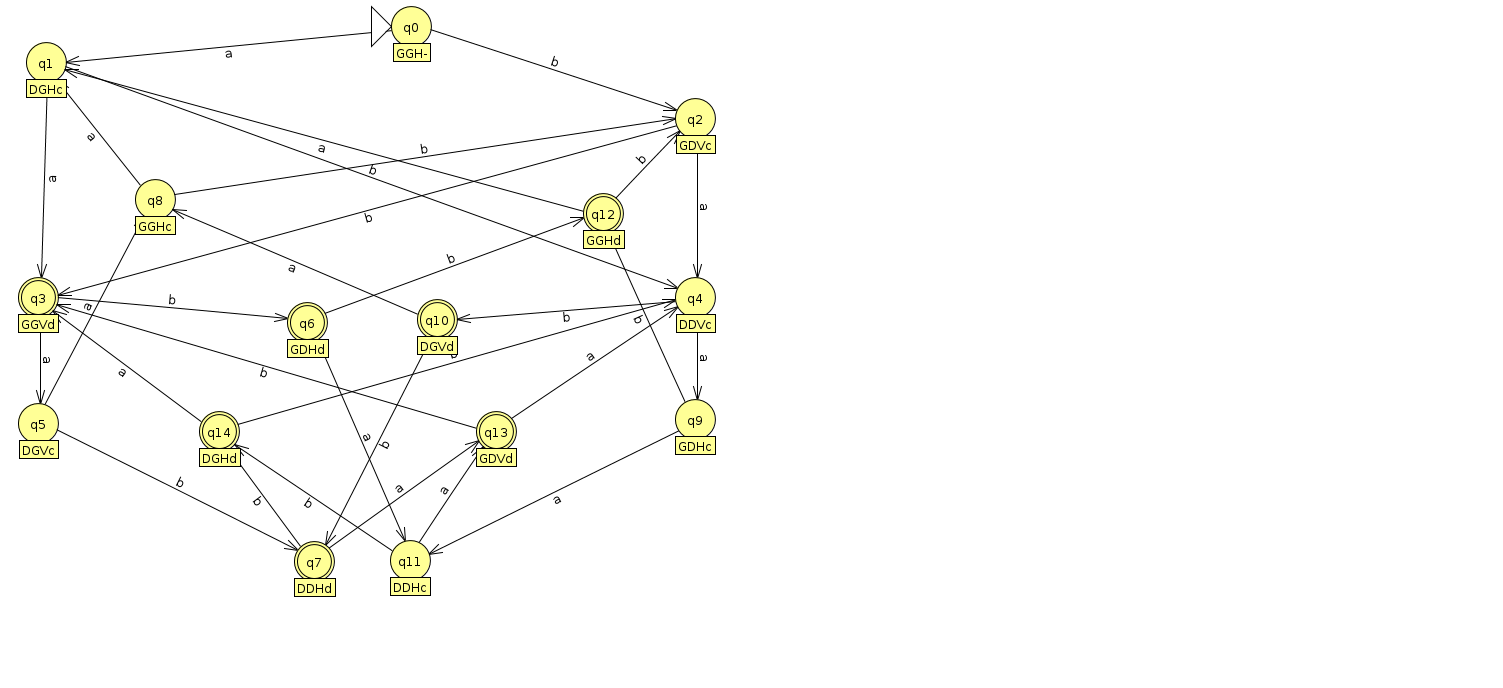
Jeu des portes bascules
Les parties gagnantes avec trois billes AAB, ABB, BAB, BBB.
Table de transition de l'automates
| A | B | |
|---|---|---|
| 000a | 100r | 011r |
| 000a | 100r | 011r |
| 001a | 101r | 011r |
| 010r | 110r | 000a |
| 010a | 110r | 001a |
| 100r | 010r | 111r |
| 100a | 010r | 111r |
| 101r | 011r | 100a |
| 101a | 011r | 100a |
| 110r | 000a | 101a |
| 110a | 000a | 101a |
| 111r | 001a | 110a |